[Activity] 7 : Stereometry

Activity 7 : Stereometry

For this activity, we would construct a 3-d image of a volume object given some of its 2D images/views. The image/views should have little differences in the position of the pixels. These small differences would be used to calculate depth information, information that will add an additional dimension to the 2D image.

We start with the following 2 input images of the same object. It is assumed that the vertical position of the pixels remain the same and the change only comes from the horizontal position pof the pixels.

Input images

The following illustration shows how the depth can be computed from the difference of the location of a certain pixel. Here, we know the difference in the distance (b), the focal length of the camera that we used (f) and the pixel locations of a point in the image (x1, x2)

The following equation show how, from the difference in coordinate values of the pixel, we could compute the depth 'z'. We use here the theory behind similar triangles.

Equations to calculate for depth

After doing the calculations, the computed 3D image for the 2 input images above are shown below. It seems that the corners has been properly reconstructed though the sides of the cube aren't as planar as hoped. This can be accounted to less than perfect matching of the pixels in the first and second image.

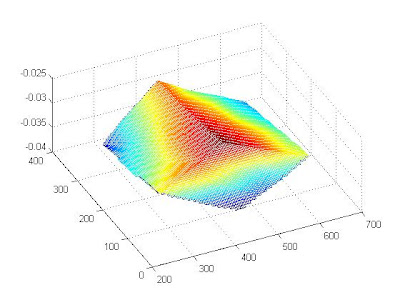
Final 3D reconstruction image

Code Listing

function stiryo

load calibdata;

b = 2.54; % the length between two points, 1 inch

Aparams = reshape(A, 3, 4);

Amat = Aparams(1:3,1:3);

Aparams = rq(Amat);

K = Aparams ./ Aparams(3,3);

focal = K(2,2) / K(1,1);

bf = b * focal;

image1 = imread('im1.jpg');

image2 = imread('im2.jpg');

newimage = zeros(size(image1));

% for i=1:1:37

imshow(image1);

[x1, y1] = ginput

close all

imshow(image2);

[x2, y2] = ginput

close all

% end

save

load cubecoords.mat

x1 = round(x1);

x2 = round(x2);

y1 = round(y1);

x = linspace(min(x1), max(x1), 100);

y = linspace(min(y1), max(y1), 100);

[X, Y] = meshgrid(x,y);

z = bf ./ (x2 - x1);

Z = griddata(x1,y1,z,X,Y,'linear');

size(X)

size(Y)

size(Z)

mesh(X,Y,Z)

end

I give myself a grade of 9.5 for this activity for achieving the objectives but wasn't able to get perfect results. The sides are not as perfectly flat as desired.

References

[1] Activity 7: Stereometry Activity Sheet, M. Soriano, Physics 305